Intersection homology, Part I
This series of posts is a quick intro to the idea of intersection homology, based on a talk I gave in a learning seminar on perverse sheaves. The first post serves as a kind of motivation for studying intersection homology. Most of the ideas are from Laurentiu Maxim’s Intersection Homology & Perverse Sheaves.
Four fun facts and four frustrating failures of ordinary homology of complex projective varieties
1. Poincare duality
For a nonsingular $n$-dimensional complex projective variety $X$, we have an isomorphism
\[\begin{align*} H^i(X; \mathbb{Z}) &\xrightarrow{\sim} H_{2n-i}(X; \mathbb{Z})\\ \omega &\mapsto \omega \frown [X] \end{align*}\]which yields the equality of Betti numbers $b_i := h^i(X; \mathbb{C}) = h^{2n-i}(X; \mathbb{C}) =: b_{2n-i}$. This is no longer true for a singular $X$. For example, suppose $X$ is the subvariety of $\mathbb{C}P^2$ given by $xy = 0$ i.e $X$ is topologically the wedge of two 2-spheres, $X \simeq S^2 \vee S^2$.
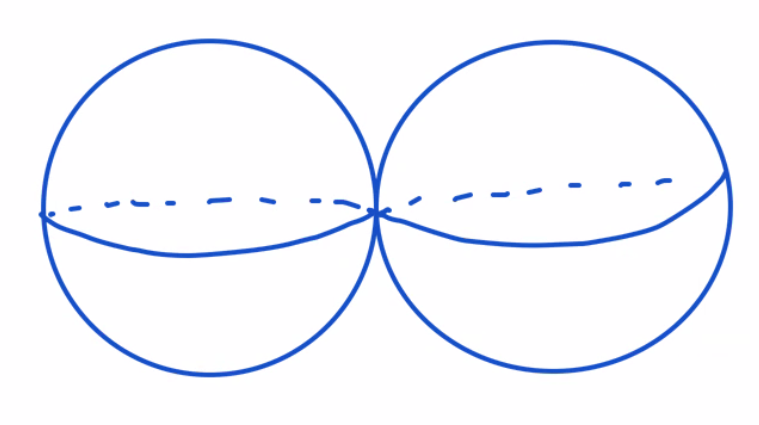 $X = S^2 \vee S^2$
$X = S^2 \vee S^2$
Using the open sets $U := X \setminus \{ [1:0:0] \}$ and $V := X \setminus \{ [0:1:0] \}$, a Mayer-Vietoris argument shows that $b_0 = 1$, $b_1 = 0$ and $b_2 = 2$. So Poincare duality fails.
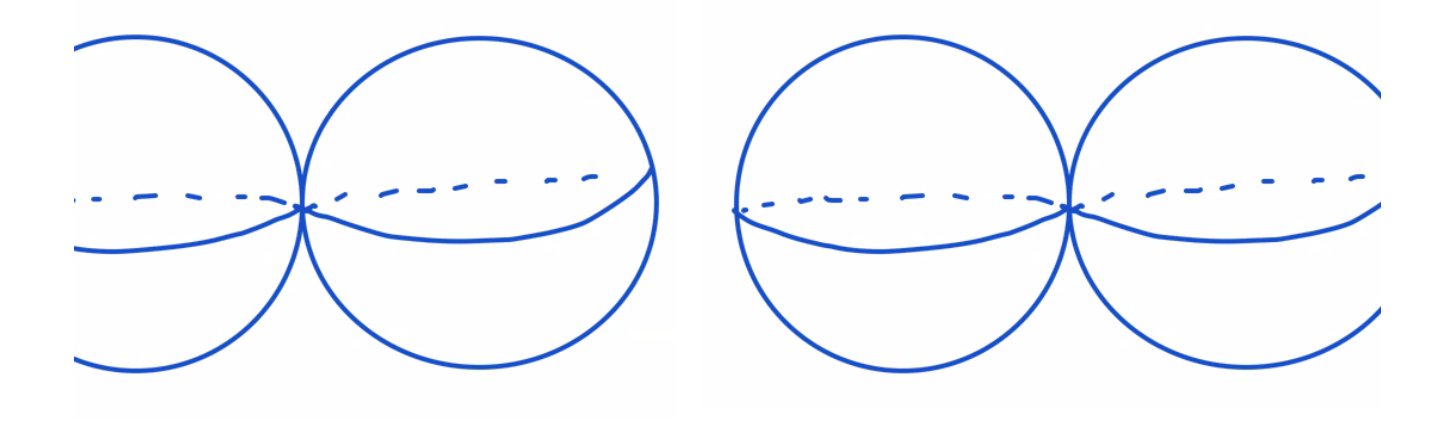 $U$ and $V$
$U$ and $V$
2. Hodge decomposition
For nonsingular $X$, we have the Hodge-de Rham isomorphism and Hodge decomposition
\[\begin{align*} H^i(X, \mathbb{C}) &\simeq H^i_{DR}(X; \mathbb{C})\\ &\simeq \bigoplus_{p+q=i} H^{p, q}(X) \end{align*}\]with $H^{q, p}(X) \simeq \overline{H^{p, q}(X)}$ (by conjugation). As a consequence of this, the odd-dimensional Betti numbers of $X$ are even. Now suppose $X$ is the zero locus of $x^3 + y^3 - xyz$ in $\mathbb{C}P^2$. The map
\[\begin{align*} \mathbb{C}P^1 &\to X\\ [x_0:x_1] &\mapsto [ x_0^2 x_1 : x_0 x_1^2 : x_0^3 + x_1^3 ] \end{align*}\]is an isomorphism on $\mathbb{C}P^1 \setminus \{[0:1], [1:0] \}$, and maps $[0:1]$ and $[1:0]$ to the same point, $P := [0:0:1]$, the singular point of $X$. Alternatively, one can think of $X$ as the degeneration of the family (for $t$ small enough) of smooth elliptic curves
\[x^3 + y^3 + t z^3 = xyz\]as $t \to 0$. Either way, $X$ looks something like this:
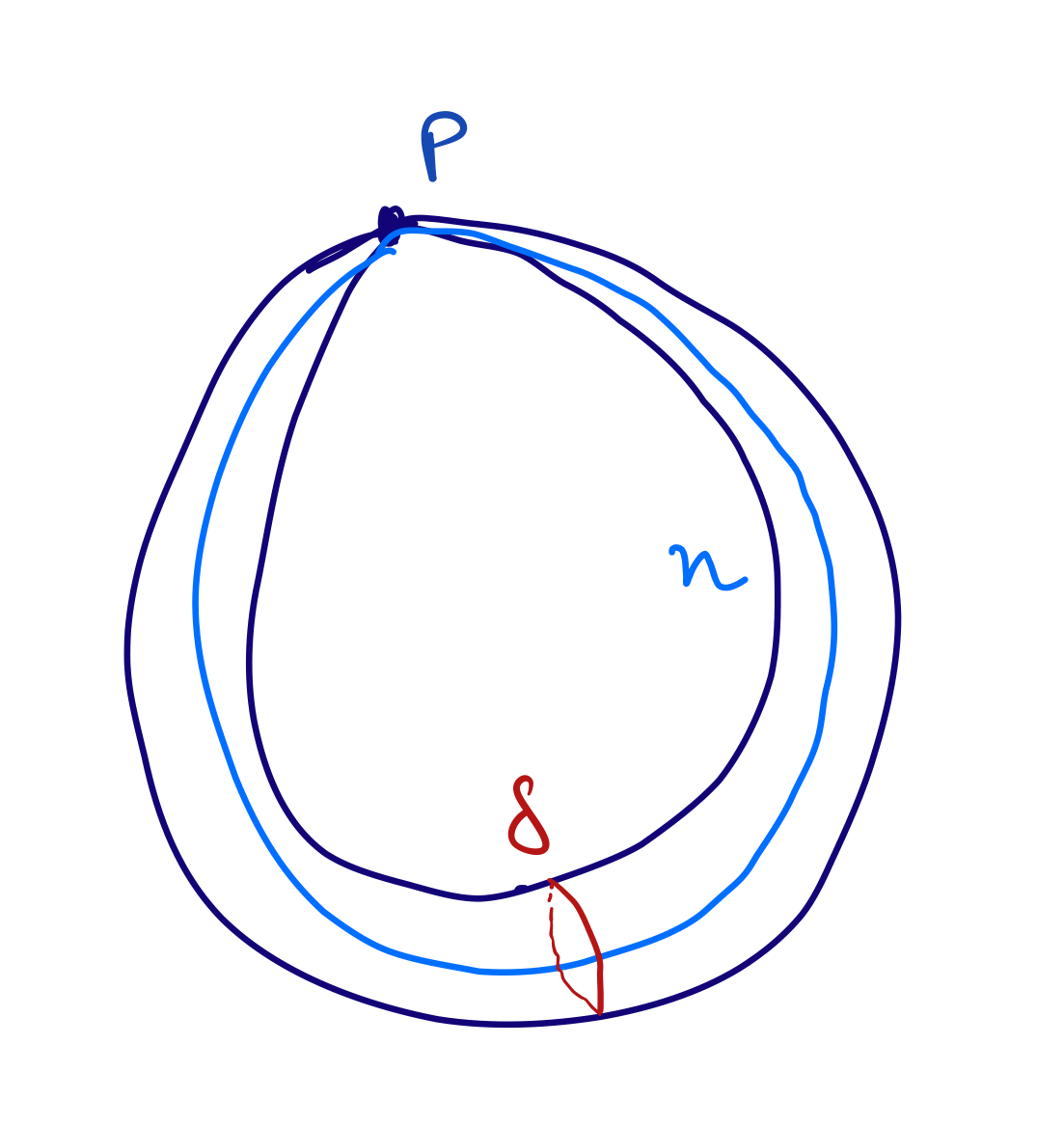 The degenerate torus, or pinched sphere, $X$
The degenerate torus, or pinched sphere, $X$
Then $b_1(X) = 1$, as can be seen from a Mayer-Vietoris argument, or by observing that $\eta$ in the picture is a cycle which is not a boundary, while $\delta$ is. In particular $X$ has an odd-dimensional Betti number that is not even, so Hodge decomposition fails for this $X$.
3. Lefschetz Hyperplane Theorem
For $X \subset \mathbb{C}P^N$ an $n$-dimensional nonsingular subvariety of $\mathbb{C}P^N$ and $H$ a generic hyperplane in $\mathbb{C}P^N$, the Lefschetz Hyperplane Theorem states that the map
\[H^i(X; \mathbb{C}) \to H^i(X \cap H; \mathbb{C})\]is an isomorphism for $i \lt n-1$ and injective for $i = n-1$. Consequently, for $n \geq 2$, if $X$ is connected (i.e $b_0(X) = 1$), then so is $X \cap H$.
Now suppose $X$ is the subvariety of $\mathbb{C}P^4$ obtained as the zero locus of the set of equations
\[\{ x_0 x_3, x_0 x_4, x_1 x_3, x_1 x_4 \}.\]Then $X$ is the union of the subvarieties of $\mathbb{C}P^4$ given by $Y := \{ x_0 = x_1 = 0 \}$ and $Z := \{ x_3 = x_4 = 0 \}$, i.e $X$ is homeomorphic to $\mathbb{C}P^2 \vee \mathbb{C}P^2$. Let $H$ be a generic hyperplane of $\mathbb{C}P^4$. Without loss of generality, we may assume that $H$ is given by the equation
\[x_3 = \sum_{i \neq 3} a_i x_i.\]Then we have
\[\begin{align*} H \cap X &= (H \cap Y) \cup (H \cap Z)\\ &= \{ \, [x_0 : x_1 : a_0x_0 + a_1x_1 : 0 : 0] \, \} \cup \{ \, [0 : 0 : a_3x_3 + a_4x_4 : x_3 : x_4] \, \}, \end{align*}\]so that $H \cap Y$ and $H \cap Z$ won’t intersect for generic $a_1, a_2, a_3, a_4$. So $X \cap H$ is a union of two disjoint lines in $\mathbb{C}P^4$ and is therefore not connected i.e the Lefschetz Hyperplane Theorem fails for this $X$.
4. Hard Lefschetz Theorem
The hard Lefschetz thorem states that the map
\[L^i : H^{n-i}(X; \mathbb{C}) \xrightarrow{\smile [H]^i} H^{n+i}(X; \mathbb{C})\]is an isomorphism for $X$ nonsingular, where $[H]$ is the class of a hyperplane or, equivalently, the symplectic form on $X$. Since the hard Lefschetz theorem implies Poincare duality, the failure of Poincare duality for a (necessarily singular) $X$ implies the failure of the hard Lefschetz theorem. I am still looking for a good example to illustrate this that is not just a repackaging of the $S^2 \vee S^2$ example.
These four failures of ordinary homology are overcome by the theory of intersection homology, developed by Goresky and MacPherson. I will introduce this in the next post.